Electronic Journal of Biology

Keywords

Action potential,Cardiac muscle cell,Minimal electrophysiology model.

1. Introduction

Sudden cardiac death is one of the most common causes in the world,especially industrialized countries in the west. Mainly,ventricular arrhythmias are the reason of cardiac death. So,a cardiac cell model is needed for exploring the cardiac arrhythmia dynamic and manner of their correlation with cell processes like behavior of ion channels. By this time,many models have been recommended in this field [1-6].

In previous models,due to the large number of ion currents,gating coefficients and state variables,the complexity of these models are very high. For example,in study of Ten Tusscher,et al [7],the presented model has 12 currents,14 gating coefficients and 17 state variables. These model deficiencies become more visible when interaction simulation is needed for many cells [8-11]. A good instance of these deficiencies is the simulation of cardiac cells and propagation of action potential in cells.

The purpose of this paper is to compare two different methods into the generation of action potential in a minimal model of ventricular muscle cell.

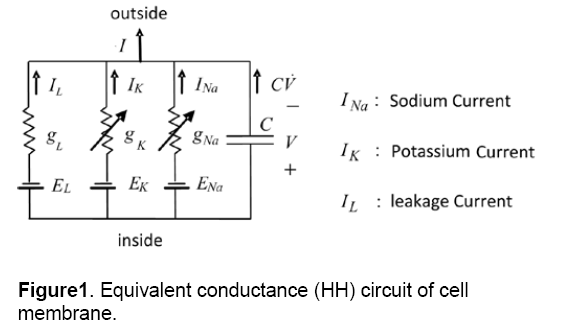
There are many models of cellular electrophysiological,but the main model of them is the conductance-based or Hodgkin-Huxley (HH) model [12]. Fig.1 shows an example of a cell model based HH. In this model,the cell membrane is shown by a few voltage sources (E),a capacitor (C) and several nonlinear conductances (g) which are dependent on voltage. Capacitor (C) is equivalent to the membrane capacitance,conductance (g) demonstrates voltage-gated and voltage source (E) is the Nernst equilibrium potential. As it is shown in this model,three ionic currents are considered for a cell. Nowadays,by the discovery of various ionic currents and ionic phenomenon in cell membrane,the numbers of the circuit branches and the element complexity of models are increasing.

Figure 1: Equivalent conductance (HH) circuit of cell membrane.

2. Methods

The minimal electrophysiology model is a pattern that has minimum numbers of state variables. In addition,it can simulate the electrophysiological behavior and performance of the cell. Figure 1 indicates an example of a minimal model with the lowest number of circuit branches and the simplest elements [13].

2.1 Introducting of INa,p +I K minimal model

Although the number and complexity of ionic currents in cardiac cells are very numerous,currents can be classified into two generic categories: inward and outward currents. Furthermore,voltage-gated that produces ionic currents are divided into two classifications: amplifying gate and resonant gate. The amplifying gate amplifies voltage changes of membrane via a positive feedback loop. It means that increasing of it will raise the voltage and raising the voltage will increase it. Resonant gate opposes voltage changes via negative feedback loop.

Opening of the gate by increasing the voltage can have two different effects. If the gate correlates with inward current,the voltage will increase (positive feedback) and if the gate is related to outward current,the voltage will decrease (negative feedback). If the gate is closed in rest state,and it opens by increasing the voltage,it will be called an activation gate. Furthermore,if the gate is open in the rest state,and it closes by increasing the voltage,it will be called an inactivation gate. A current (inward or outward) can have just one or both types of gating parameters (activation or inactivation). So,in the other word,amplifying current is an inward current with activation gate or an outward current with inactivation gate. Similarly,resonant current is an inward current with inactivation gate or an outward current with activation gate.

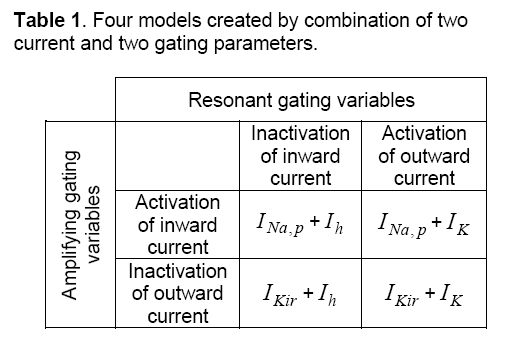
To produce a model of a dynamical system both positive and negative feedbacks are needed. The combination of two currents and two gating parameters create four minimal models. These four models are illustrated in Table 1. As shown in table INa,p,and IKirare currents with amplifying gating variables,also,Ihand IKare currents with resonant gating variables. A typical model consists of at least one amplifying and one resonant gating variable

In this paper,to produce a minimal model,an inward current with name of INap,has been chosen. The voltage-gated of this current,which is defined

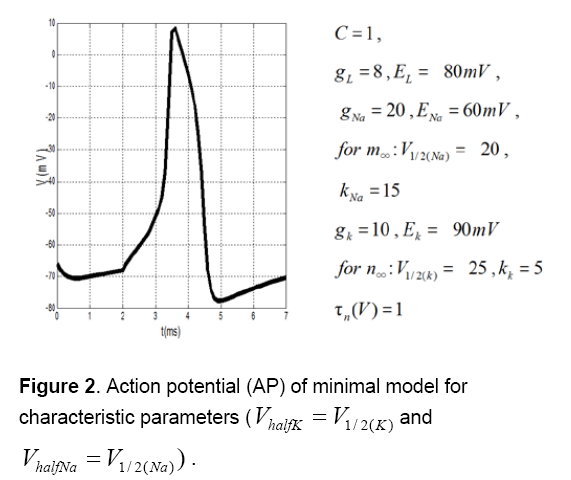
Figure 2 shows action potential (AP) of this minimal model for characteristic parameters [14,15]. Figure 3 shows that AP morphology is not as same as cardiac AP.

Figure 2: Action potential (AP) of minimal model for characteristic parameters and

Figure 3: AP diagram of electrophysiological model.

2.2 Parameters fitting

In this paper,two methods (MES method and voltage-clamp method) are examined for fitting of proposed model parameters. In next sections,these methods will be described in details.

2.2.1 Parameters fitting using MSE method.

One of the researches that have done recently in this field is the paper of Alfonso Bueno-Orovio,et al [16],that a minimal model based on four variables has indicated for APs of ventricular. However in this paper,generating of AP by using the INap +IK minimal model is so easier; also this method is using a model based on two variables. The equations of this minimal model differ with more complex ionic models. This model uses Inward and outward currents as two main categories of currents instead of using a numerous of ionic channel currents.

AP morphologies and its other properties are carefully matched in all cases by using the parameter-fitting algorithm. Model study shows that each model parameter has a particular effect on the electrophysiological properties. Thus,an initial value is considered for each parameter based on their characteristics. For example,Ek and EI represent Nernst equilibrium potentials of outward currents,so they should determine in range of membrane resting potential.

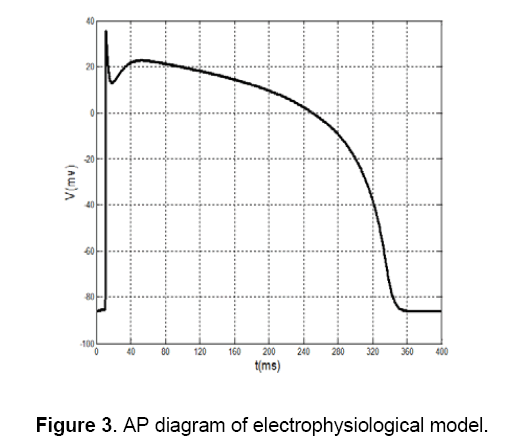
Then,by using MATLAB program the parameters will regulate in some stages. Each time that a step is being repeated,an error function can be calculated,because of the difference that causes between the square of experimental data and the proposed model. In this test,the experimental data are chosen from Ten Tusscher's electrophysiological model [7] as it is shown in Figure 3 . In this model,created error is reached to minimum value,then; the initial parameters will be fitted by using MSE method.

2.2.2 Parameters fitting using Voltage-Clamp method.

In this method,electrophysiological model of Ten Tusscher et al. [7] is used as a starting point. In the next stages by using voltage-clamp method,parameters fitted,which minimal model has the behavior as same as Ten’s model.

Tests and required measurements on this model have done by COR (Cellular Open Resource) software [17]. This software has been developed by researchers of Oxford University and containing many cellular electrophysiological models.

Moreover,for regulating of data,the MATLAB software is used

3. Results and Discussion

3.1 MSE method.

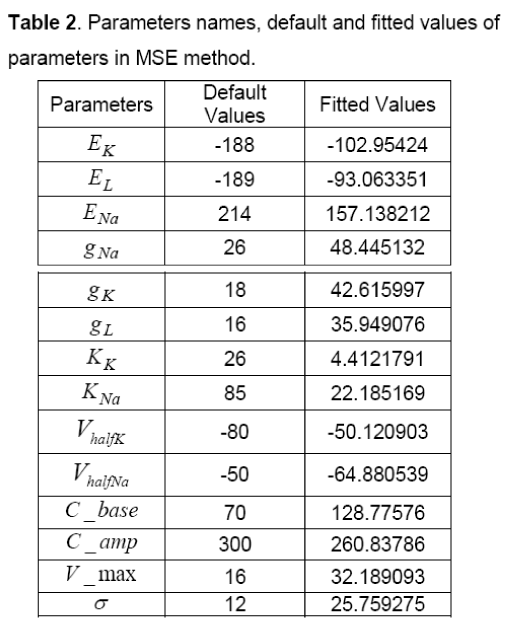
As it was mentioned before, first, default values are chosen for parameters of kpNaII+, minimal model.

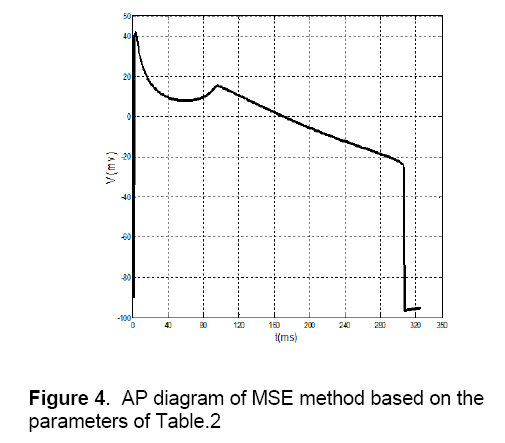
These default values are shown in Table 2. In addition to, The AP of Ten’s model has selected as a desirable AP and obtained data is extracted with two vectors, wherein the first vector shows time, and the second vector represents potential. In this method, first, by using default parameters in each specified time, potential can be calculated and its AP is generated. Then, parameters of the proposed model are fitted by comparing the Ten Tusscher’s data (Figure 3), the output of the minimal model and by using MSE method. The values of these fitted parameters are shown in Table 2. Figure 4 shows AP diagram which is based on the parameters of Table 2.

Figure 4: AP diagram of MSE method based on the parameters of Table.2

3.2 Voltage-clamp method

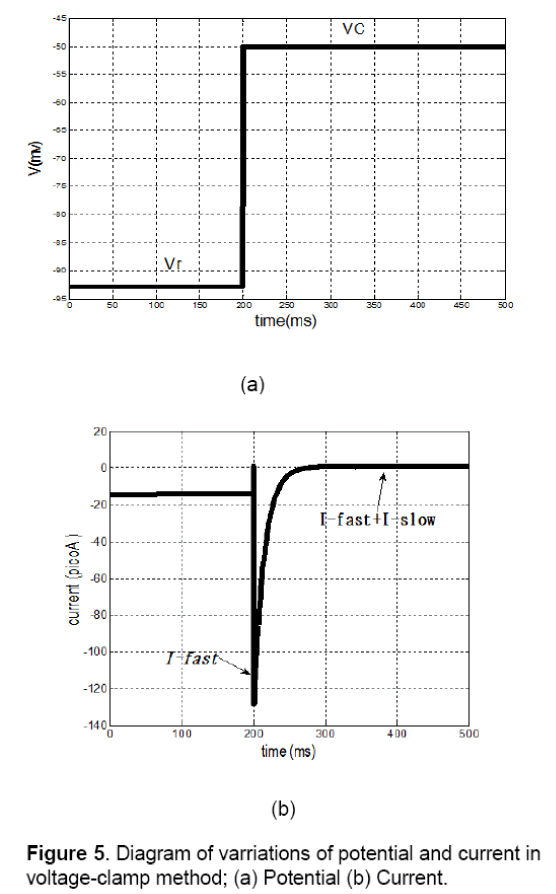
On examination of voltage-clamp method on a cell,fast or slow components of membrane current can be measured. As it is shown in Figure 5 (a),resting potential of membrane (Vr) suddenly has been shifted to Vcand has fixed in this position.

Figure 5: Diagram of varriations of potential and current in voltage-clamp method; (a) Potential (b) Current.

In this condition the membrane current has a sudden and fast change that is fastI and after a while it achieves to its final value (∞I), wherein ∞I is equivalent toslowfastII+. Changes of current are shown in Figure 5(b). In this method, both vectors of fastI andslowI can be calculated by various values of membrane potentials. The results of this test are summarized in Table 3.

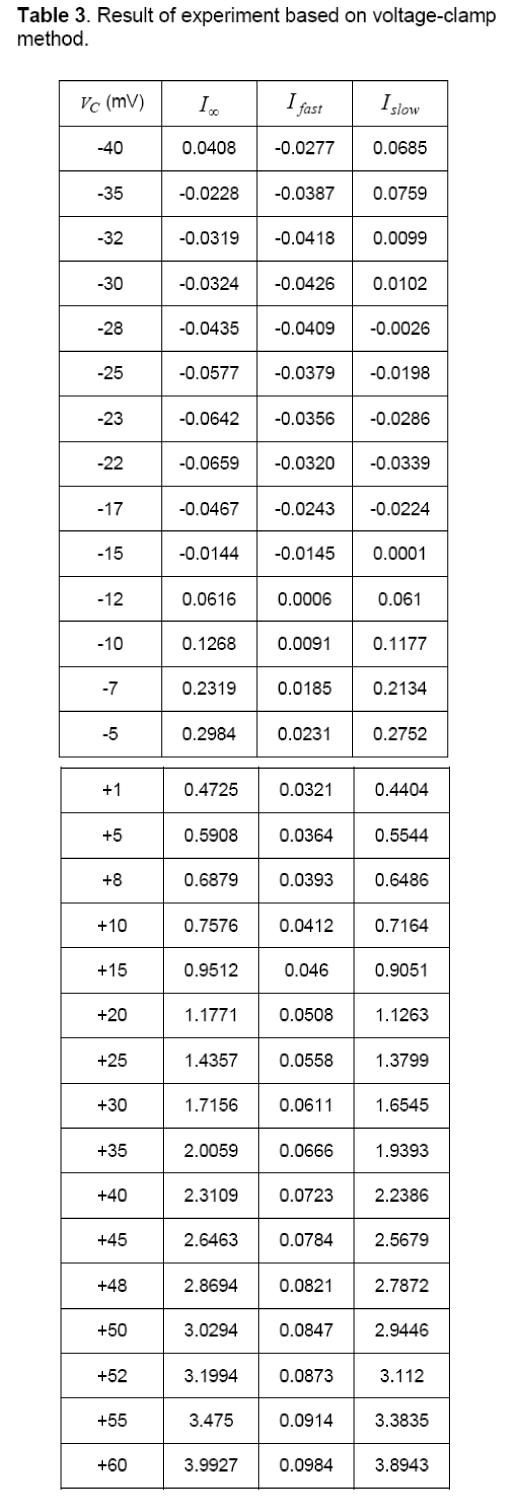
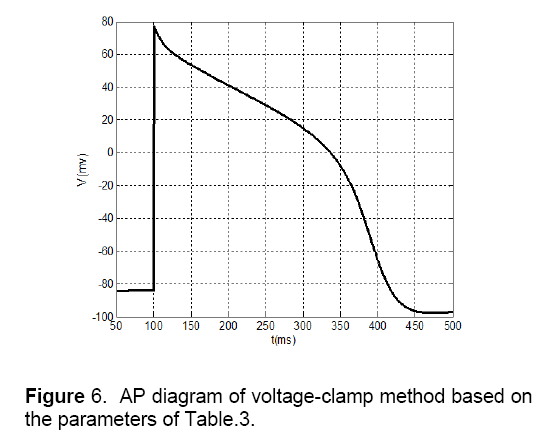
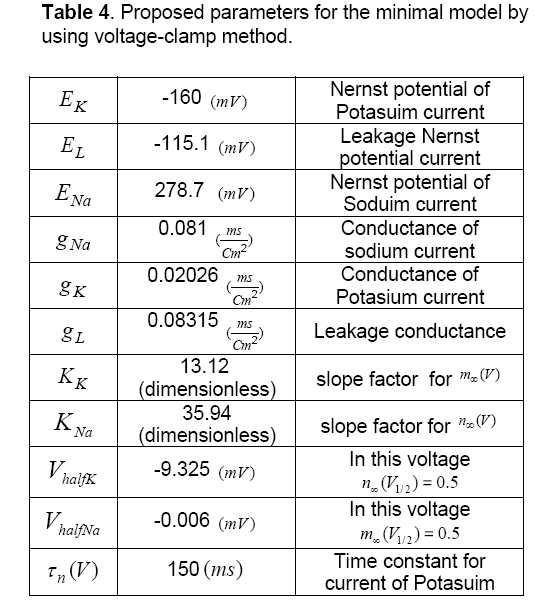
Table 4 depicts proposed parameters for the minimal model by using voltage-clamp method. Also, Figure 6 shows the AP diagram of this method.

Figure 6: AP diagram of voltage-clamp method based on the parameters of Table.3.

4. Discussions

In this paper,two methods were examined for a minimal model,and they have developed two different action potentials for cardiac muscle cell. The proposed minimal model has just two- state variables,so,computationally has less complexity of the simulation. These specifications the make model more proper for simulation of cardiac arrhythmias that has caused by dissemination of action potential like atrial fibrillation. It is predicted that this model can maintain its importance and efficiency in tissue levels of the body too.

The accuracy of the proposed model is measured by comparing its behavior with a real cell. There are many standards for specifying the model accuracy like AP morphology,excitability,all or none principle,restitution of AP and CV,etc. In continuance model accuracy has been specified by some of these standards.

The procedure of excitability and all or none principle is different with AP morphology. These standards just study on one or two properties of the model. These two standards are studied on both MSE and voltage-clamp methods and the results for both were as same as each other. So,in this paper,the accuracy of these two standards is investigated just for voltage-clamp model.

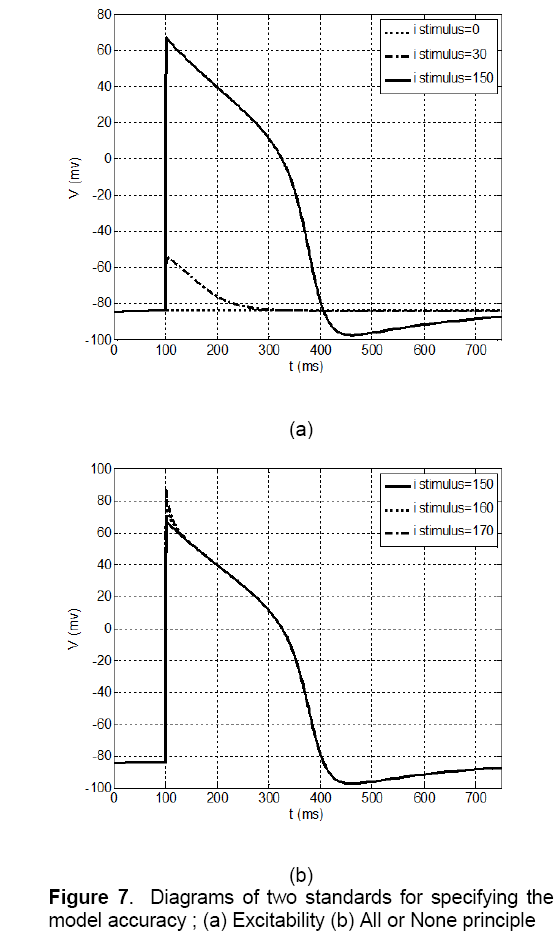
The concept of excitability in a nonlinear dynamic system such as a cell is that if the system is in a state of rest and its condition is stable,by applying a small stimulation pulse,the potential of membrane will be a little depolarized. If the excitation amplitude is less than the threshold value,the potential will return to its rest state again,and the action potential (AP) will not be generated. AP is generated only when the stimulation amplitude reaches to the threshold value. It’s observed that according to Figure 7 (a),in the proposed model,if the excitation amplitude of current becomes less than 150 Pico Ampere,the AP will not be created and if the amplitude reaches more than this value the AP will be produced certainly. So,the proposed model has the excitation property.

Figure 7: Diagrams of two standards for specifying the model accuracy ; (a) Excitability (b) All or None principle

The other criteria evaluation of model is all or none principle. According to this principle if the large stimulation applies to the cell,the cell will be stimulated and AP will be generated. In this condition if the stimulation increases,form and amplitude of AP will not change again. In the other word,shape of AP is independent of stimulation value. This issue has been studied on proposed model and its result is shown in Figure 7 (b). It can be noticed that the AP has not been generated by amplitude value of less than 150 Pico Ampere. However,if stimulation value becomes 150 Pico Ampere,AP will be created and increasing of stimulation amplitude will not make any changes in AP form. So this model has this property.

specifications of these models have compared by using the AP morphology standard like Ten Tusscher or Noble. In this comparison,most of the features like resting potential and APD are the same. However,there are some differences between generated APs in these two methods:

1. Notch potential: In Fig.4 the notch potential is about 20 mV,but this potential in fig.6 is about 5 mV.

2. Amplitude of potential: In Figure 4 amplitude of potential is about 40 mV,and this value approximately is as same as the value of Ten’s model in Figure 3 . This fact doesn’t match for voltage-clamp method (Figure 6 ).

3. Phase 2 of AP: As shown in Fig.3 there is an overshoot with a mild slope in phase 2 of the diagram. This case can be observed in MSE method (Figure 4 ) too. The diagram of voltage-clamp method (Figure 6 ) doesn’t have any overshoot in phase 2 and its potential value decreases with steady velocity.

4. Phase 3 of AP: In phase 3,the diagram of voltage-clamp method (Figure 6 ) is more similar to Fig.3 than diagram of MSE method (Figure 4 ). As shown in Figure 3 and Figure 6 in phase 3,but in Figure 4 this event occurs instantaneously.

5. Conclusion

From these comparisons,it can be concluded that in AP morphology,standard MSE method (Figure 4 ) is matched to Ten’s method (Figure 5 ) more than voltage-clamp method (Figure 6 ). The Proposed model by using MSE method has more accuracy and efficiency in comparison with other models that have been presented before,like Alfonso’s model,etc. This model has a few numbers of currents and state variables. So,because of its simplicity and high speed of tissue simulation,it will be considered soon. It seems that the only problem with this model is its difference of slopes with Ten’s model in some areas,which by more effort,this problem will be fixed.

Acknowledgements

This study was supported by the grant of the Romanian Academy of Science.

References

1. Hall A.E.,Hutter O.F. and Noble D. (1963) Current-voltage relations of Purkinje fibers in sodium-deficient solutions. Journal of Physiology. 166: 225–240.
2. Beeler G.W.,Reuter H. (1977) Reconstruction of the action potential of ventricular myocardial fibers. Journal of Physiology. 268: 177–210.
3. Luo C.,Rudy Y. (1991) A model of the ventricular cardiac action potential. Depolarization,repolarization,and their changes. Circulation Research. 68: 1501–1526.
4. Hutter O.F. and Noble D . (1960) Rectifying properties of heart muscle. Nature. 188: 495.
5. Noble D. (1965) Electrical properties of cardiac muscle attributable to inward-going (anomalous) rectification. J Cell Comp Physiol. 22: 127–136.
6. Noble D.,Varghese A.,Kohl P. and Noble P. (1998) Improved guinea-pig ventricular cell model incorporating a dyadic space IKr and IKs and length and tension-dependent processes. Canada Journal of Cardiolog. 14: 123–134.
7. Ten Tusscher K.H.W.J.,Noble D.,Noble P.J. and Panfilov A.V. (2004) A model for human ventricular tissue. Am J Physiol. 286: 1573–1589.
8. Fenton F.H.,Cherry E.M.,Hastings H.M.,Evans S.J. (2002) Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos .12: 852–892.
9. Keener J.,Sneyd J. (2004) Mathematical Physiology. Springer Science and Business Media: New York.
10. Sachse F.B. (2004) Computational Cardiology. Springer: Berlin.
11. Clayton R.H.,Panfilov A.V. (2008) A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Progress in Biophysics and Molecular Biology. 96: 19–43.
12. Hodgkin A.L.,Huxley A.F. (1952) A quantitative description of membrane current and its application to conductance and excitation in nerve. Journal of Physiology. 117: 500–544.
13. Esmaeili S. and Sabzposhan S.H. (2012) Modelling the ventricular muscle cell by the least parameters,Asian Journal of Biomedical and Pharmaceutical Sciences. 2(10): 15-19
14. Izhikevich Eugene M. (2003) Simple model of spiking neurons. IEEE transactions on neural networks. 14: 1569-1572.
15. Wang G. and Jiang P. (2006) Tristability in model neurons. IEEE international conference on neural networks. Vancouver.
16. Bueno A.,Cherry E.M.,Fenton F. (2008) Minimal model for human ventricular action potentials in tissue,Journal of Theoretical Biology. 253: 544-560.
17. COR. Cellular Open Resource. https://cor.physiol.ox.ac.uk.